
Great Thanks to Tina Nye (A-5; 05-06) for much work on graphics: making a rough idea reality!
Chemical equilibrium
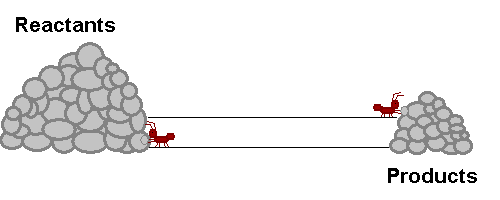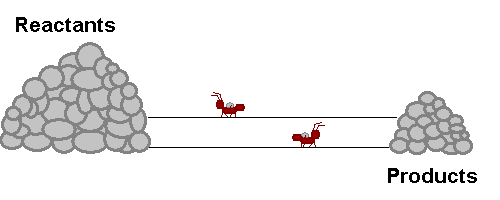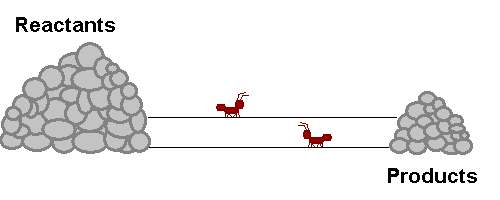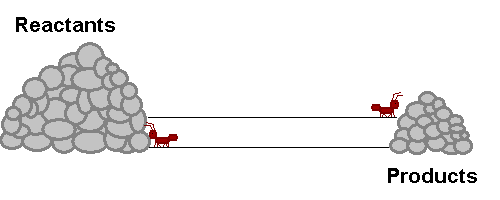
A system in equilibrium is like our ants up there! As long as the ants work at the same speed, the piles of sand remain in equilibrium. Neither gets bigger or smaller (It is important to note however that the piles are not the same size!). The work that each ant does exactly offsets what the other is doing. Products are being stacked up and the same rate that they are being taken away. Reactants are being stacked up at exactly the same rate that they are being taken away. If this were a chemical reaction, reactants would be colliding to make product at the same rate that products would be colliding with each other to make fresh reactant again! The reaction never really stops, but the forward reaction and reverse reaction proceed and the same rate, so we don't see a change in the size of the piles! Nifty Huh!!!!?
Chemical equilibrium is reached when the rates for the forward and reverse chemical reactions are equal for a chemical system. Or you could say when products are being made as fast as they are breaking down to form reactants again. The concentrations of products and reactants are generally NOT EQUAL.
To know what the concentrations are, you use the Equilibrium Constant
expression (Keq).
Keq = [products]/[reactants]. Its a ratio : ) So Keq > 1 favors products, Keq < 1 favor reactants.
For a general equation like:
wA + xB <===> yC + zD
Remember, the square brackets mean concentration, in molarity, if it is given in some other unit you must calculate molarity. Coefficients in the chemical equation become exponents in the Keq expression. Leave out any solids or pure liquids since they have undefined molarities ; ).
Keq= If you spend time with the following notes, you'll master this topic in no time.
Predicting final concentrations and cheating while were doing it.
- Balanced eqn :H2 + I2 <===> 2 HI Given H2=I2= 0.200 M and Keq = 0.64
- ICE table:
| H2 | I2 | HI | |
| Initial | 0.200 | 0.200 | 0 |
| Change | 0.200-x | 0.200-x |
2x |
| Equilibrium | .20-.08 = .12 | .20-.08 = .12 | .16 |
| Revise cheating | only if | negative |
Keq = [HI]2
[H2] [I2]
Le Chatelier's Principle
A chemical system, once it as equilibrium will respond to a stress or change in the environment by responding to reduce the stress.
A complete set of notes including familiar examples.
Le Chatelier's Principle notes.
Ionization of Acids and Bases: Ka & KbStrong acids or strong bases always disassociate (ionize) 100%, we really aren't going see much of them in this unit. Weak acids and weak bases on the other hand like to stay together as molecules, they don't disassociate very much.
The measure of how "strong" an acid is is given by Ka. The measure of how "strong" a base is is given by Kb. A high Ka means that you get more ionization so produce more H3O+ (hydronium) in a solution with water. More hydronium means you have a "stronger" acid.
Ka = [products]/[reactants]
Kb = [products]/[reactants]
Acids when ionized, always separate at the H+, bases at the
OH-. Also remember, square brackets mean concentration in molarity.
Sample Problem
If Ka is 3.5 x 10-8 what is the [H+] in a 0.050M solution of
HClO?
1) Chemical
Equation for ionization of hypochlorous acid: HClO <---> H+ +
ClO-
2) Ka expression (no numbers): Ka = [H+][ClO-]/[HClO]
( Well will always leave out the -x term in the denominator. Our
justification is that Ka will always be small so x will be small and we can
ignore the quadratic without causing too much grief : )
3) Substitute and solve:
let x stand for both [H+]and [ClO-] then
x2/0.050 = 3.5 x 10-8.
x = 4.2 x 10-
5M
The Solubility Product: Ksp
Ksp comes from Keq, only this time our reactants are solid so they get left out. That is because for a solid concentration is meaningless. I mean the solid is 100% solid but there is no solvent so you are sort of dividing by 0 to try to get concentration.
Ksp= [Products]
Steps in solving problems
1. Write a balance dissolving equation.
Ex: Al(OH)3 <---> Al3+ + 3OH- (Leave the polyatomics
together, split the compound between the metal and the anion).
2. Write a Ksp expression (no numbers yet).
Ex: Ksp = [Al3+][OH-]3 (Coefficients become
powers, and are on the outside of the brackets. The charges are on the inside of
the brackets are just part of the ion's label, not really numbers at
all.)
3. NEW, NEW, NEW: Substitute X for ion according to mole ratio. If X =
Al3+ , then OH- = 3X because they are 1:3 in the balanced chemical equation.
Substitute into Ksp expression.
Ex: Ksp = (x)(3x)3 (Exponent is on outside of parenthesis, so
cube 3x first then multiply by x)
Then Ksp = 27x4
From here you could solve for X (molar solubility) given KSP or you could solve
for the numerical value of Ksp given X (molar solubility)
Common Ksp's are:
x2 ( Mole ratio 1:1)
4x3 (Mole ratio 1:2, or 2:1)
27x4 (Mole ratio 1:3, or 3:1)
108x5 (Mole ratio 2:3 or 3:2)
if you have some other solution for Ksp, check your algebra.
A thorough text heavy set of notes.
Predicting Precipitation
Predicting whether precipitation occurs boils down to one question. Is my ION PRODUCT
(Qip) greater than the KNOWN SOLUBILITY PRODUCT (KSP)?
Qip > Ksp then precipitation.
Ksp > Qip no precipitation.
Sample problem
The final concentration of
CaCl2 in a solution is 1.5 x10-5 M and the final concentration of NaF in a solution
AFTER mixing is 2.2
x10-2 M Will precipitation occur?
Ksp of CaF2 is 4.0 x10-11
Step 1: Write a balanced dissolution reaction.
(Hint: if you're not sure what will form, read the question carefully, the known Ksp of the compound must be given. That is what might or might not form depending on the ION PRODUCT).
Ex. CaF2 <--> Ca2+ + 2F-
Step 2: Write a Ksp expression but call it Qip
(it will have our data in it, from the concentrations that we put
together in a test tube.)
Ex:Qip = [Ca][F-]2
Step 3: Subsitute the ACTUAL VALUES of the concentrations of the ions that we actually have.
No X's
because we have no unknowns. We just want to see if our ion product is greater than the known
Ksp. If so, the solution can't hold that many ions and precipitation occurs.
Ex: Ca2+ = 1.5 x10-5 M and F- = 2.2 x10-2 M
(from the problem)
Kip= [Ca2+] [F-]2
Substituting
Qip = (1.5 x10-5)(2.2 x10-2)2
Hint: raise to power 1st)
Qip = 7.26 x10-9
Ksp = 4.0 x10-11
Qip is 180x more than Ksp so we get a precipitate or GUNK in the bottom of test tube.
Remember negative exponents are fractions 10-9 is bigger than 10-11

Looks like Qip is greater than Ksp!!!